- Home
- Schulen
- Lernmaterial
- ROBOTICS Base Set
Grundlagen der Robotik begreifbar machen und nachhaltig verstehen!
Das fischertechnik Robotics TXT 4.0 Base Set ist der perfekte Start, um zu programmieren wie die Profis! Der umfangreiche Baukasten enthält neben der Kamera mit Bildverarbeitung einen Ultraschallsensor, zwei Encodermotoren, einen Spursensor, einen Fototransistor sowie zwei Taster und zwei LEDs. Die Modelle können mit der grafischen Programmiersoftware ROBO Pro Coding und dem ROBOTICS TXT 4.0 Controller programmiert und gesteuert werden. Einsteiger können auf fertige Beispielprogramme zurückgreifen, Fortgeschrittene und Profis können direkt in einer Blockly-Programmierumgebung oder in Python loslegen. Enthalten sind 12 spannende Modelle, die von der Fußgängerampel über eine Schranke, einen Barcodescanner bis hin zu mobilen Fahrrobotern mit Encodermotoren, Kamera, Spur- und Abstandssensor reichen. Das umfangreiche Lehrmaterial beinhaltet neben Einführungs- und Basisinformationen 20 Experimente mit Lösungen zu den 12 Modellen.

Nachfolgend kann der Bildungsplanbezug des Produkts je Bundesland eingesehen werden. Thema, Lernziele, Zeitaufwand und Bildungsplanbezug pro Aufgabe finden Sie über den Download des didaktischen Begleitmaterials.
|
Land |
Stufe |
Fächer / Bezüge |
|
BW |
SEK 1 |
IMP 8-3.1.1.2 Algorithmen (1), S. 28ff; INFWF 8-3.1.2 Algorithmen (1), S. 15; INFWF 9-3.2.2 Algorithmen (2), S. 21; INFWF 9-3.3.2 Algorithmen (2), S. 28 |
|
BY |
SEK 1 |
RS- IT 2.7.1 Logische Schaltungen - Regeln und Steuern durch Sensorauswertung, S.698; RS- IT 2.7 Logik und Robotik, S.699; GYM 9/10 LPLUS INF - Modellieren, Implementieren, Anwenden, Softwareprojekte |
|
BE |
SEK 1 |
INF-3.5 Algorithmisches Problemlösen, S. 25; INF-3.9 Physical Computing (Wahlthemenfeld), S. 27 |
|
BB |
SEK 1 |
INF-3.5 Algorithmisches Problemlösen, S. 25; INF-3.9 Physical Computing (Wahlthemenfeld), S. 27 |
|
HB |
SEK 2 |
GYM OS INF-Algorithmen und Datenstrukturen, S. 6; GYM OS INF-Imperative Programmierung, S. 7 |
|
HH |
SEK 1 |
GYM 7/8 INF-M1 Informatik strukturieren und präsentieren, S. 18 |
|
HE |
SEK 2 |
GYM KCGOINF-E1/E2 Einführung in die Informatik, S. 26 |
|
MV |
SEK1 |
GYM 5 INF-3 Programmieren? Kinderleicht!, S.16; GYM 8 INF-3 Sensorgesteuerte Anwendungen entwickeln, S.25; GYM 9 INF-3 Sensorwerte erfassen und auswerten, S.28; |
|
NI |
SEK1, 2 |
Pflichtfach ab 2023/2024; KC-INF LF Computerkompetenz, S.18; SEK 2 KC-INF IK3 Informatiksysteme und ihre zugrundeliegenden Modelle, S.12; |
|
NW |
SEK 1, 2 |
RS 9/10 WPF TECHNIK 2.3 Inhaltsfeld 7: Kommunikations- und Digitaltechnik S.23; 5/6 KLP INF - Information und Daten, S. 17; 5/6 KLP INF - Informatiksysteme, S. 18; SEK 2 KLP GOS INF - 2 Algorithmen, S. 21 ff |
|
RP |
SEK 1 |
IPS 5 INF - Informatiksysteme und Netze, S. 7; IGS/GYM INF-2.1 Grundlagen der Informationsverarbeitung, S. 17 |
|
SL |
SEK 1, 2 |
GYM 9 INF - Algorithmik, S. 3; GYM OS INF GOS-Funktionsweise von Computersystemen, S.9ff. |
|
SN |
SEK 1 |
OS 6 TC-WB4 Signale nutzen, S.12; GYM 5/6, TC-WB5 EVA-Prinzip bei Einplatinenrechnern, S.9 |
|
ST |
SEK 1 |
GYM 9, INF 3.2 Algorithmen interpretieren und entwickeln, S.15 |
|
SH |
SEK 1, 2 |
INF KB4 Kommunikation, S. 10; INF KB5 Informatiksysteme, S. 11; FA Physik, Variabilität (…Sensoren zur Messerfassung) S.13; SEK 2 INF4.4.3 Messen. Steuern, Regeln, S. 37 |
|
TH |
GYM 10 INF - 2.3 Algorithmen, S. 14 ff.; GYM 10 INF 2.5.1 Technische Informatik, S. 18ff. |
Computer sind aus unserer modernen Welt nicht mehr wegzudenken. Sie umgeben uns nicht nur in Gestalt von PCs, Laptops oder Tablets: Wir tragen sie als Smartphones in der Hosentasche, sie stecken in unseren Autos, in Spül- und Waschmaschinen, in der Heizungssteuerung, in E-Bikes und in Kaffeeautomaten.
Jahr für Jahr werden sie leistungsfähiger und zugleich immer kleiner und kompakter. Damit nehmen auch ihre Einsatzfelder zu, denn sie können nun auf die jeweilige Anwendung zugeschnitten und als „eingebettete Systeme“ (embedded systems) in diese integriert werden. Sie erfassen und „vermessen“ mit Sensoren ihre Umgebung und steuern Motoren, LEDs oder andere Aktoren. Durch moderne Funk-Kommunikationstechniken wie WLAN oder Bluetooth können sie miteinander vernetzt werden und Daten untereinander oder mit einer Steuerzentrale austauschen.
Wie aber funktionieren solche eingebetteten Systeme und ihr jeweiliges „Herzstück“, der Mikroprozessor? Was ist ein Mikrocontroller und wie werden damit Sensordaten erfasst und ausgewertet? Wie steuert man mobile Systeme, z. B. Roboter oder Fahrzeuge? Wie können die Systeme miteinander kommunizieren und Daten austauschen?
In dieser Lerneinheit steht das Verständnis von Mikrocontrollern und deren Einsatz im Zentrum. Es werden die zentralen Grundlagen erläutert und in deren praktische Umsetzung in den Übungen (Aufgaben) vertieft. Dabei werden verschiedene wichtige Einsatzbereiche von Mikrocontrollern vorgestellt: Messung, Kommunikation, Codierung und Verschlüsselung, Steuerung und Regelung, Robotik und autonomes Fahren.
Definition
Unter einem Mikrocontroller versteht man ein Steuerungssystem aus einem Mikroprozessor und einer Anzahl Ein- und Ausgänge. An den Eingängen werden Sensoren oder Speicher angeschlossen, an den Ausgängen Aktoren wie beispielsweise Motoren, LEDs oder Displays. Mikrocontroller verfügen über einen flüchtigen Arbeitsspeicher (RAM), der beim Ausschalten gelöscht wird, und meist auch über ein EEPROM, in dem Programme und Daten dauerhaft gespeichert werden können. Im Unterschied zu Laptops und PCs gibt es weder eine Tastatur als Eingabe- noch einen Bildschirm als Ausgabe-Einheit; diese müssen separat angesteuert werden.
Bekannte und verbreitete Vertreter solcher Mikrocontroller sind z. B. der Arduino, der BBC micro:bit, der Calliope Mini und der TXT Controller von fischertechnik.
Das Herzstück des Mikrocontrollers ist ein Mikroprozessor. Für sich betrachtet ist ein Mikroprozessor ein Integrierter Schaltkreis (IC), der aus einem (temporären) Speicher – Random Access Memory (RAM) genannt – Befehle und Daten in die Register des IC lädt, in einer Recheneinheit verarbeitet und das Ergebnis wieder im RAM ablegt. Ein Mikroprozessor besteht im Wesentlichen aus Transistoren – elektronischen „Schaltern“, die genau zwei Zustände kennen: „Ein“ und „Aus“. Mit diesen Transistoren lassen sich logische Schaltungen konstruieren wie „Und“-, „Oder“- und „Nicht“-Verknüpfungen. Die Ergebnisse werden in einen „Flipflop“, einem stabilen Wechsel-Schalter gespeichert (Näheres dazu im Education-Kasten „Electronics“).
Ein Quarz gibt dem Mikroprozessor den Takt vor, also die Geschwindigkeit, in der der Mikroprozessor die Befehle und internen Rechenschritte abarbeitet. Die Befehle werden in einem (je nach Mikroprozessor-Typ unterschiedlichen) Maschinencode angegeben und bestehen aus einem Kommando (bspw. „addiere zwei Werte“) und, je nach Befehl, mehreren Parametern (bspw. den beiden zu addierenden Werten oder den Registern, in denen die Werte gespeichert sind).
Die Leistung des Mikroprozessors wird bestimmt durch die Taktgeschwindigkeit, die Datenbreite in Bit (die angibt, wie groß die Adressen und Werte sein dürfen, die die Mikroprozessorbefehle in einem Schritt verarbeiten können) und dem Maschinencode selbst: Je komplexer die Befehle, die der IC ausführen kann, desto schneller in der Regel die Datenverarbeitung. Zur Beschleunigung der Zugriffe auf das RAM enthalten viele Mikroprozessoren heute einen eigenen Cache-Speicher, in dem sie Befehle und Daten während der Verarbeitung zwischenspeichern.
Die heute in Laptops und PCs eingesetzten Mikroprozessoren können 64 bit lange Daten (Werte, RAM-Adressen) verarbeiten, enthalten mehrere Milliarden Transistoren und werden mit mehreren GHz (Milliarden Schwingungen pro Sekunde) getaktet. Sie können sich die Arbeit teilen („Multi-Core“) und verfügen über viele Megabyte große Cache-Speicher. In Mikrocontrollern werden heute meist Mikroprozessoren mit einer Wortbreite von 32 bit und einer Taktfrequenz unter einem GHz genutzt – das ist bei Weitem ausreichend für die Aufgaben eines Mikrocontrollers.
Historie
Seit der Antike experimentieren die Menschen mit Automaten – Konstruktionen, die, angetrieben von Luft oder Wasserkraft, selbständig Arbeiten verrichten, vorgegebene Bewegungsabläufe auf Kommando ablaufen lassen oder auch Musik erzeugen. Im 15. Jahrhundert n. Chr. konstruierte Leonardo da Vinci (1452-1519) zahlreiche Maschinen, die in Theatern und Fürstenhöfen Volk und Adel beeindruckten. Wolfgang von Kempelen (1734-1804) baute 1791 einen funktionsfähigen Sprachsyntheseapparat. Als erster „programmierbarer Automat“ gilt die 1805 von Joseph-Marie Jacquard (1752–1834) entwickelte Lochkartensteuerung für mechanische Webstühle.
Der Durchbruch für die Entwicklung flexibel einsetzbarer Steuerungen gelang jedoch erst mit der Entwicklung des Computers. Durch die Erfindung des Integrierten Schaltkreises (IC) im Jahr 1958/1959 durch Jack Kilby (1923-2005) und Robert Noyce (1927-1990) und die Entwicklung des Mikroprozessors im Jahr 1971, erfunden und patentiert von Ingenieuren der Firma Texas Instruments, wurden sehr flexible, leichte, schnelle und verschleißfreie, vor allem aber programmierbare Steuerungen möglich. Der erste Mikroprozessor, der TMS1000, enthielt 8.000 Transistoren. Die Zahl der Transistoren eines Mikroprozessors verdoppelt sich seitdem etwa alle 18 Monate. Diese Entwicklung wird auch nach Gordon Moore (*1929), der diesen Zusammenhang 1965 aus der Weiterentwicklung von ICs in den vorausgegangenen Jahren ableitete, „Mooresches Gesetz“ genannt. Heutige Mikroprozessoren bestehen aus mehreren Milliarden Transistoren – und sind dabei kaum größer als der TMS1000.
Wie wird ein Mikrocontroller programmiert?
Die Programmierung des Mikrocontrollers erfolgt in der Regel nicht auf dem Mikrocontroller selbst, sondern in einer speziellen Programmier- oder Entwicklungsumgebung (integrated development environment, IDE) auf einen PC, Laptop, Tablet oder auch einem Smartphone. Damit erstellte Programme werden dann über eine Kommunikationsschnittstelle, z. B. USB, WLAN oder Bluetooth, in den Speicher des Mikrocontrollers übertragen und dort ausgeführt.
Genau so wird auch der TXT 4.0 programmiert: Die Programme werden in ROBO Pro Coding auf einem PC, Laptop oder Tablet in der Programmiersprache Blockly oder Python entwickelt und dann auf den TXT 4.0 übertragen, auf dem sie ausgeführt werden.
Was ist ein "endlicher Automat"?
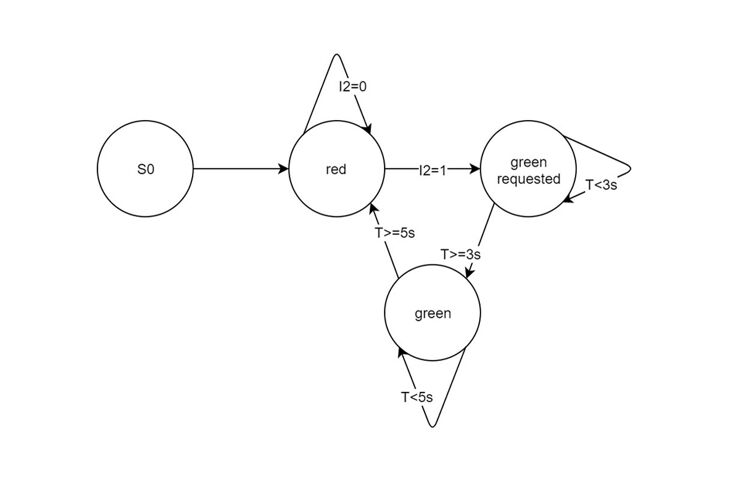
Als „endlicher Automat“ wird ein System bezeichnet, dessen Verhalten sich als eine endliche Menge von Zuständen beschreiben lässt. Der Übergang von einem Zustand in einen anderen wird dabei von Bedingungen (wie z. B. Ereignissen, beispielsweise Werteänderungen von Sensoren) ausgelöst, auf die jeweils eine Aktion folgt. Endliche Automaten werden daher auch „Zustandsmaschinen“ genannt und durch Zustandsübergangsdiagramme beschrieben.
Endliche Automaten spielen eine wichtige Rolle bei der Beschreibung von Mikrocontrollern: Fast jedes eingebettete System (wie z. B. eine Aufzugsteuerung oder ein Roboter) lässt sich als ein System aus endlich vielen Zuständen verstehen. Die Darstellung als Zustandsübergangsdiagramm vereinfacht das Verständnis des Systems meist erheblich und erleichtert eine (vor allem fehlerfreie) Programmierung. Denn in jedem Zustand sind nur die Ereignisse zu berücksichtigen, die zu einer Zustandsänderung führen, wie bspw. die Anforderung eines „Grün“-Signals an einer Fußgänger-Bedarfsampel (siehe das Beispiel in der Abbildung).
Was sind analoge und digitale Daten?
Mikrocontroller können nur „Ein“- und „Aus“-Zustände verarbeiten, also binäre Werte, die zwei verschiedene Zustände annehmen können. Die Auswertung von Sensoren, die ebenfalls nur zwei Zustände kennen, wie Taster, Reed-Kontakt (Magnetschalter) oder Fototransistor, ist daher sehr einfach, und der Zustand des Sensors kann als digitales Datum in einem Bit gespeichert werden.
Aber in der Wirklichkeit gibt es natürlich nicht nur binäre Zustände. So können beispielsweise Helligkeit, Temperatur oder Entfernungen sehr viele unterschiedliche Werte annehmen. Solche analogen Daten können wir auch mit Sensoren messen, wie z. B. einem Fotowiderstand, einem Thermistor (Heißleiter) oder einem Ultraschall-Abstandssensor. Damit unser Mikrocontroller diese analogen Werte verarbeiten kann, muss er sie allerdings in Zahlen, also in digitale Daten umwandeln. Das sind allerdings komplexere Werte als die binären, die uns die digitalen Sensoren liefern: Aufbauend auf den binären Zuständen kann der Mikroprozessor unter Verwendung des Dualsystems alle Zahlenwerte darstellen (und durch eine geeignete Kodierung auch andere Zeichen, wie z. B. Buchstaben, aber dazu später).
Die Umwandlung des analogen Sensorwerts in eine Zahl (also ein komplexeres digitales Datum) übernimmt in einem Mikrocontroller ein Analog-Digital- (A/D-)Wandler: Der anliegende Sensor-Wert, meist ein elektrischer Widerstand oder eine Spannung, wird dazu elektronisch „abgetastet“. Ist der Widerstand oder die Spannung hoch, liefert der A/D-Wandler einen großen Zahlenwert; ist der anliegende analoge Wert niedrig, ist der an den Mikrocontroller gelieferte Zahlenwert klein. Wie präzise der am Eingang anliegende analoge Wert bestimmt werden kann, hängt von der Auflösung des A/D-Wandlers ab. Die wird üblicherweise in der Bit-Länge des Ergebniswerts angegeben.
Die acht Eingänge des TXT 4.0 Controllers können sowohl als digitale (binäre) als auch als analoge Eingänge genutzt werden. Die A/D-Wandler an den Eingängen tasten analoge Werte wie beispielsweise den elektrischen Widerstand des Heißleiters, der sich abhängig von der Temperatur ändert, mit einer Genauigkeit von 12 bit ab, wandeln den Widerstand also in eine Zahl zwischen 0 und 4096 um. Durch unterschiedliche Referenzspannungen können beim TXT 4.0 sogar nicht nur Widerstände im Messbereich von 5 kOhm, sondern auch deutlich größere Widerstandswerte recht präzise bestimmt werden.
Was ist Nebenläufigkeit?
Unter Nebenläufigkeit versteht man die Eigenschaft eines Systems, verschiedene Prozesse gleichzeitig (oder „parallel“) abzuarbeiten. Die Nebenläufigkeit wird (technisch) entweder durch eine Verteilung der Prozesse auf mehrere Mikroprozessoren („Multi-Core“) umgesetzt, oder indem der Mikroprozessor durch Multitasking die Prozesse schrittweise abwechselnd abarbeitet, sodass der Eindruck einer echten Parallelität entsteht.
Nebenläufige Prozesse eignen sich besonders gut für die Programmierung voneinander unabhängiger Abläufe oder Ereignisse, vor allem dann, wenn einer oder mehrere der Prozesse zeitabhängig in einem festen Rhythmus erfolgen (wie beispielsweise ein Blinklicht). Um nebenläufige Prozesse aufeinander abzustimmen (zu synchronisieren) verwendet man „Semaphore“: Das sind meist beiden Prozessen zugängliche Variablen, über deren Wert die Prozesse einander beispielsweise ihren Status mitteilen oder aufeinander warten können.
Wie bestimmt man mit einem Heißleiter die Temperatur?
Ein Heißleiter (auch Thermistor oder NTC-Widerstand genannt) ist ein Widerstand, dessen Widerstandswert sich abhängig von der Temperatur ändert. Heißleiter haben einen negativen Temperatur-Koeffizienten (NTC), d. h. mit steigender Temperatur sinkt der Widerstandswert. Die folgende Grafik zeigt die Widerstandskennlinie des fischertechnik-Heißleiters.
Der fischertechnik-Thermistor hat bei 25°C einen Widerstandswert von 1,5 kOhm. Wie an der Grafik zu erkennen ist die Kennlinie des Heißleiters nicht linear. Aber man kann den Temperaturwert einigermaßen genau über eine lineare Kurve annähern. Dazu muss man einen zweiten Messwert bestimmen und daraus die Gleichung der linearen Funktion berechnen.
Der fischertechnik-Thermistor hat bei 25°C einen Widerstandswert von 1,5 kOhm. Wie an der Grafik zu erkennen ist die Kennlinie des Heißleiters nicht linear. Aber man kann den Temperaturwert einigermaßen genau über eine lineare Kurve annähern. Dazu muss man einen zweiten Messwert bestimmen und daraus die Gleichung der linearen Funktion berechnen.
Für eine genauere Berechnung des Temperaturwerts T (in Kelvin) aus dem Widerstandswert R eines NTC-Widerstands wird üblicherweise die folgende Steinhart-Hart-Gleichung verwendet:
1/T=a+b(lnR)+c(lnR)³
Die Temperatur in °C erhält man aus T durch Subtraktion von 273,15.
Mit zwei zusätzlichen Messwerten (neben dem Widerstandswert von 1,5 kOhm bei 25°C) können wir ein Gleichungssystem mit den drei Unbekannten a, b und c aufstellen. Dieses Gleichungssystem müssen wir nicht selbst lösen: Auf der Webseite von Stanford Research Systems gibt es einen „Thermistor Calculator“, der uns aus den drei Messwerten die gesuchten Parameter der Steinhart-Hart-Gleichung berechnet.
Wie funktioniert der Ultraschall-Sensor?
Die Abstandsmessung erfolgt durch die Aussendung von mehreren 200 µs langen 40 kHz-Signalen (im von Menschen nicht hörbaren Spektrum) und der Messung der Zeit bis zum Empfang deren Echos, also den von einem Objekt reflektierten Schallwellen. Aus der Laufzeit der Echo-Signale lässt sich der Abstand über die Schallgeschwindigkeit wie folgt berechnen. Für die Schallgeschwindigkeit (in Luft) gilt:
c = (331,5+0,6∙t/°C) m/s
Bei Zimmertemperatur (t=20°C) liegt c also bei etwa 343,5 m/s oder 0,03435 cm/µs. Um aus der Signallaufzeit (in µs) den Abstand in cm zu erhalten, muss man sie zunächst durch zwei teilen und dann mit 0,03435 multiplizieren – oder gleich durch 58,224 dividieren. Diese Arbeit übernimmt ein IC auf dem Ultraschall-Sensor und liefert den Abstand in cm; auch der Einfluss der Temperatur auf die Messung wird von dem Sensor automatisch kompensiert.
Die Reichweite des Ultraschall-Sensors liegt bei ca. 4 m. Bei Zimmertemperatur vergehen also 400 ∙ 58,224 = 23,3 ms, bis das Echo des Trigger-Signals von einem 4 m entfernten Objekt zurückkehrt. Erreicht in dieser Zeit kein Echo den Sensor, liefert er als Ergebnis den Wert „0“ zurück (kein Objekt in Reichweite). Die durch die Laufzeit des Signals bedingte Verzögerung muss man bei einem mobilen System (wie z. B. einem Fahrzeug) in der Steuerung berücksichtigen.
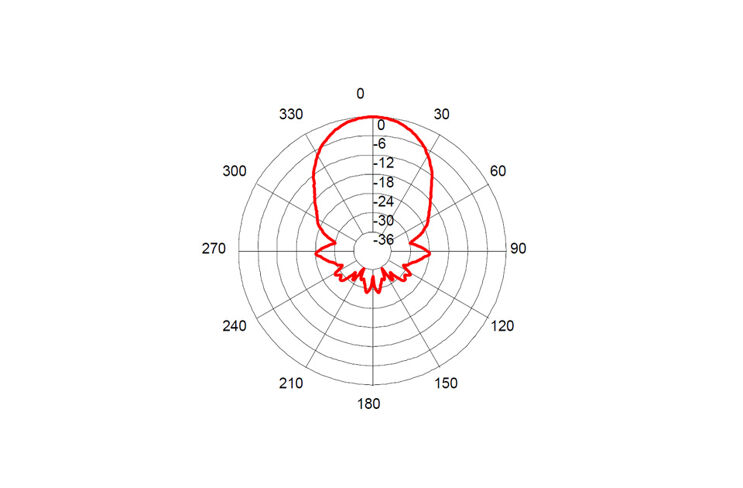
Schallwellen breiten sich kreisförmig aus, daher hat der Sensor eine gewisse Streuung. So erkennt er nicht nur unmittelbar vor ihm liegende Hindernisse, sondern auch seitlich positionierte Objekte (siehe Abbildung).
Schließlich muss man beachten, dass die Echos den Sensor nur dann erreichen, wenn die Schallwellen in einem nicht zu spitzen Winkel auf das Objekt treffen. Das kann man leicht experimentell überprüfen.
Was ist ein Code?
Ein Code ist – ganz allgemein – eine Vereinbarung über die eindeutige Darstellung von bestimmten Informationen. Codes werden benötigt für die Übermittlung, aber auch für die Anzeige von Informationen. Jedem Zeichen eines Codes ist dabei eine bestimmte Bedeutung zugeordnet. Codes, die uns täglich begegnen, sind z. B. die (arabischen) Ziffern zur Darstellung von Zahlen oder die Schriftsprache zur Darstellung von Wörtern und Sätzen. Andere Codes sind die Noten auf Notenlinien zur Darstellung von Tonhöhe und Tondauer oder die Schaltzeichen in Schaltplänen zur Darstellung elektronischer Bauelemente. Immer dann, wenn Menschen Informationen für andere Menschen dokumentieren oder untereinander austauschen möchten, benötigen sie einen Code, den sowohl der Sender als auch der Empfänger kennt.
Codes spielen aber nicht nur zwischen Menschen eine wichtige Rolle: Auch Computer können ohne Codes keine Informationen austauschen, weder mit Menschen noch untereinander. Codes, die von Computern verwendet oder verstanden werden, müssen dabei besonders klar und eindeutig sein, damit es nicht zu Missverständnissen kommt. Daher werden viele Codes so gestaltet, dass Fehler, z. B. durch eine Störung bei der Übertragung, erkannt werden können. Es gibt sogar Fehler erkennende Codes, die bestimmte Fehler korrigieren können.
Wie kommunizieren Computer?
Will man mit Hilfe von Mikrocontrollern „kommunizieren“, so muss man die Informationen (Nachrichten) zunächst in Daten umwandeln, die der Mikrokontroller übermitteln soll. Die Nachricht kann dabei so gut wie alles sein: ein Text, ein Bild, Musik, Sprache. Für die Übermittlung müssen diese Informationen kodiert werden. Dazu müssen sich Sender und Empfänger auf eine Kodierung einigen, die beide kennen – in der Praxis sorgen technische Standards dafür.
Der aus der Kodierung resultierende Datenstrom kann dann über Töne (Schallwellen), sichtbare Zeichen, elektrische Ströme in einer Leitung, als Lichtimpulse in einer Glasfaserverbindung oder als elektromagnetische Welle „durch die Luft“ übermittelt werden. Die Flaggensignale auf einem Flughafen, Sirenensignale oder ein Feueralarm, E-Mails, Chats, Telefongespräche, Videokonferenzen, Smartphone-Navigation – alles das sind Beispiele für eine Kommunikation von in einer vereinbarten Kodierung dargestellten Informationen.
Wie funktionieren Barcodes?
Ein Barcode ist ein „Balkencode“ oder Strichcode, der aus schwarzen und weißen senkrechten Balken verschiedener Breite besteht. Barcodes zählen zu den eindimensionalen Codes, da die Information allein in der Breite der Balken enthalten ist (bspw. schmaler Balken = „0“, breiter Balken = „1“). Die Farbe der Balken (s/w) dient allein deren Unterscheidung. Barcodes sind „optische Codes“, d. h. sie können von einem Sensor, der „hell“ und „dunkel“ unterscheiden kann, oder von einer Kamera mit Bildauswertung gelesen werden. Barcodes werden überwiegend zur Kennzeichnung von Objekten verwendet; man findet sie z. B. auf Büchern und Zeitschriften (ISBN/ISSN), auf Waren-Etiketten oder Aufklebern für die Paketpost. Es gibt sehr viele unterschiedliche Barcodes, die sich durch ihre Informationsdichte und durch die verwendeten Prüfziffern unterscheiden. Barcodes haben den Vorteil, dass sie sehr robust sind und leicht eingelesen werden können; auch sind die Lesegeräte sehr günstig.
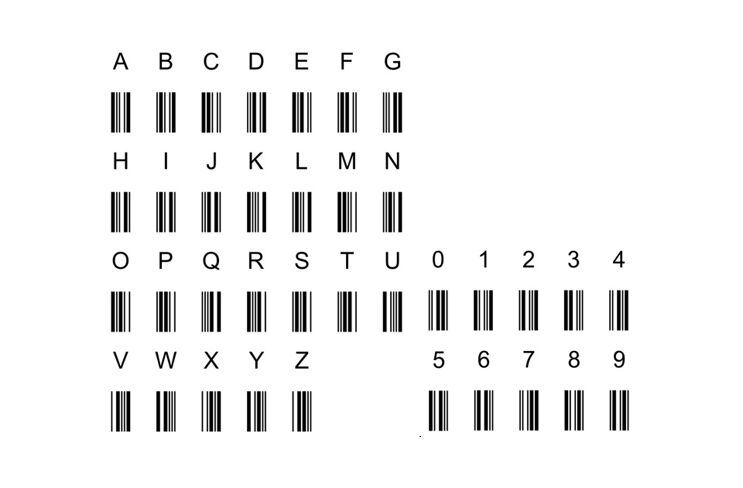
Ein typischer Barcode ist der Code 39. Er wurde bereits 1973 bei der Fa. Intermec entwickelt und inzwischen von diversen Normungs-Organisationen (darunter ANSI und ISO) in Spezifikationen bzw. Normen festgelegt (u. a. der ISO/IEC 16388). Ein Code-39-Zeichen besteht aus neun Balken – fünf schwarzen und vier weißen (den Zwischenräumen) – in zwei verschiedenen Breiten. Dabei steht ein breiter Balken für eine „1“ und ein schmaler für eine „0“; ein Code-39-Zeichen entspricht also einer neunstelligen Binärzahl.
Vor und hinter jedem Zeichen folgt ein (schmaler) weißer Zwischenraum, damit man die einzelnen Zeichen unterscheiden kann. Code-39-Barcodes sind immer gleich breit, denn die Anzahl der breiten Balken je Zeichen ist auf genau drei festgelegt: zwei schwarze und ein weißer. Ein Code-39-Zeichen besteht also immer aus sechs schmalen und drei breiten Balken, oder sechs „0“-en und drei „1“-en. Der Code-39-Standard definiert insgesamt 44 Zeichen: die 26 Buchstaben des Alphabets, die zehn Ziffern „0“ bis „9“ und die acht Sonderzeichen „*“ (Start-/Stoppzeichen), Leerzeichen, „-“, „+“, „.“, „/“, „%“ und „$“.
Eine Weiterentwicklung der Barcodes sind QR-Codes, die aus Punkten auf einer quadratischen Fläche bestehen. Sie zählen zu den zweidimensionalen Codes und erfordern eine Kamera zum Einlesen und Dekodieren.
Was ist der Morse-Code?
Einer der ersten „technischen“ Codes, mit dem Zeichen durch Maschinen lesbar gemacht wurden, war der Morsecode, entwickelt 1838 von Alfred Vail (1807-1859), einem Mitarbeiter Samuel Morses (1791-1872), und erstmalig standardisiert im Jahre 1865. Der Morse-Code stellt Ziffern und die Buchstaben des Alphabets als unterschiedliche Folgen kurzer („Dit“) und langer („Dah“) Signale dar. Er kann daher nicht nur für die elektrische Telegrafie eingesetzt werden, sondern auch andere Signale wie Lichtzeichen, Töne oder Striche zweierlei Länge verwenden und ist damit vollständig unabhängig von der Übertragungstechnik.
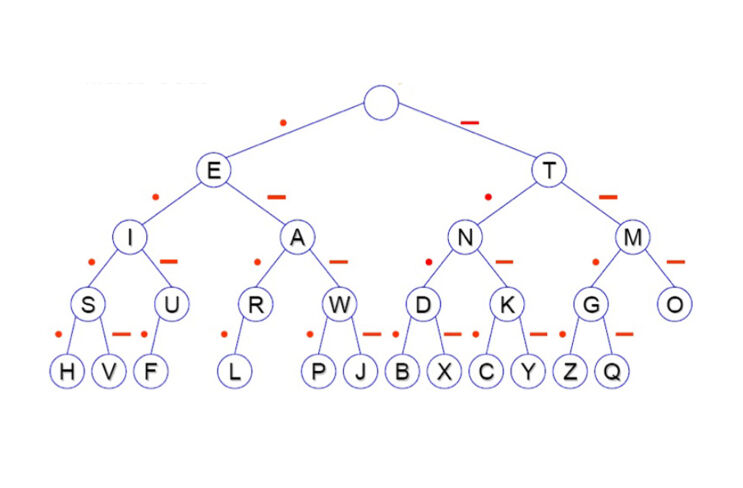
Die Kodierung der Buchstaben des Alphabets zeigt der folgende Code-Baum. Ein „E“ wird mit einem „Dit“, ein „A“ mit einem „Dit“ gefolgt von einem „Dah“ und ein „N“ mit einem „Dah“ gefolgt von einem „Dit“ kodiert. Die Zeichen des Codes sind damit unterschiedlich lang.
Damit besitzt der Morse-Code eine weitere sehr wertvolle Eigenschaft: Er ist sehr effizient, denn er verwendet kurze Signalfolgen für häufig genutzte Buchstaben und längere für seltene und kompensiert damit teilweise die Redundanz natürlicher Sprachen.
Die Länge eines „Dah“ entspricht dabei der Länge von drei „Dit“. Zwischen zwei Symbolen wird eine Pause von einem „Dit“ Länge gesendet, zwischen zwei Buchstaben eines Wortes eine Pause von drei „Dit“ Länge, und zwischen zwei Wörtern eine Pause von sieben „Dit“ Länge. Die Übertragungsgeschwindigkeit wird durch die Länge eines „Dit“ festgelegt.
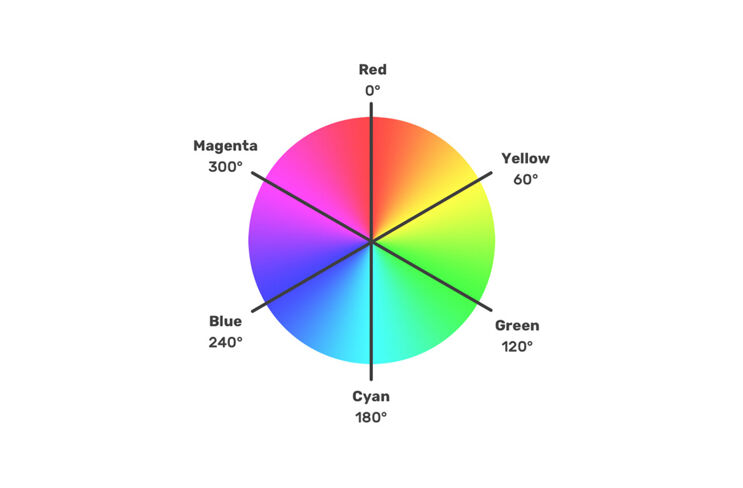
Wie funktioniert der RGB-Farbcode?
Der RGB-Code ist eine Drei-Byte-Kodierung der Farbanteile R (Rot), G (Grün) und B (Blau, jeweils von 0-255) in einem Farbton. Aus einem RGB-Wert kann der Farbton (Hue) wie folgt bestimmt werden:
Als Ergebnis erhält man den Winkel, in dem diese Farbe im Farbkreis liegt (siehe Abbildung).
Was ist Redundanz?
Als Redundanz bezeichnet man in der Informationstheorie Daten, die man ohne Informationsverlust weglassen kann. Ein Code ist redundant, wenn er mehr Bits benötigt als für die Darstellung der verschiedenen Zeichen minimal erforderlich wären. Wenn alle Zeichen des Codes gleich lang sind, gibt die Anzahl der zusätzlichen, für die Informationsdarstellung eigentlich nicht benötigten Bits des Codes dessen Redundanz an. Wenn wir beispielsweise ein einfaches 1/0-Signal kodieren möchten, benötigen wir dafür zwingend lediglich ein Bit. Kodieren wir das Signal jedoch mit den Ziffern „1“ und „0“ (als ASCII-Zeichen), so benötigt unser Code acht Bit. Die Kodierung hat also eine Redundanz von sieben (Bit):
Redundanz = log₂ (Anzahl mögliche Codeworte/Anzahl zu kodierender Zeichen)
In unserem Beispiel beträgt die Redundanz also log₂ (2⁸/2) = log₂ (2⁷) = 7.
Wie funktioniert Verschlüsselung?
Die Verschlüsselung von Daten (auch Chiffrierung genannt) dient dazu, den Inhalt einer Nachricht zwischen Sender und Empfänger geheim zu halten und ein „Mitlesen“ Unberechtigter wirksam zu verhindern. Dafür werden Verschlüsselungsverfahren verwendet, die die Nachricht in einer zwischen Sender und Empfänger vereinbarten Weise „verändern“. Dabei wird möglichst nicht das Verschlüsselungsverfahren selbst geheim gehalten, sondern lediglich ein nur Sender und Empfänger bekannter Schlüssel („Kerkhoff’sches Prinzip“). Meist werden dabei die Zeichen der Nachricht durch andere ersetzt (substituiert) oder untereinander vertauscht (permutiert).
Früher wurden vor allem einfache Substitutions-Chiffren verwendet. Eines der bekanntesten Verfahren ist die so genannte „Caesar-Chiffre“. Dabei werden die zu übermittelnden Buchstaben der Nachricht im Alphabet um eine feste Anzahl Stellen (dem Schlüssel) „verschoben“. So wird beim Schlüssel „3“ aus einem „A“ ein „D“, aus einem „B“ ein „E“ und so weiter, bis aus einem „Z“ schließlich ein „C“ wird. Die Entschlüsselung beim Empfänger erfolgt genau umgekehrt.
Eine Caesar-Verschlüsselung ist leicht zu knacken, denn die Häufigkeitsverteilung der Buchstaben einer natürlichen Sprache wird durch die Verschlüsselung nicht verändert: Bei einem längeren Text ist der mit Abstand häufigste Buchstabe das „E“. Kennt man den häufigsten Buchstaben des verschlüsselten Textes, so weiß man, um wie viele Stellen man das Alphabet „verschieben“ muss, um den mitgehörten Text zu entschlüsseln.
Außerdem gibt es nur 25 verschiedene Möglichkeiten, die Buchstaben im Alphabet zu verschieben: Das ist eine sehr geringe Anzahl möglicher Schlüssel. Man könnte also auch so lange verschiedene Verschiebungen durchprobieren, bis beim Entschlüsseln ein sinnvoller Text herauskommt.
Deutlich schwieriger zu knacken ist eine von Blaise de Vigenère (1523-1596) im Jahr 1586 veröffentlichte Verschlüsselung, bei der die Zeichen der Nachricht nicht alle um die gleiche Anzahl Stellen im Alphabet verschoben werden, sondern nach einem vorgegebenen Schema. So bedeutet der Schlüssel „1 5 12 4 8 7 11“, dass das erste Zeichen der Nachricht um eine Stelle, das zweite um fünf, das dritte um 12 usw. und schließlich das siebte um 11 Stellen im Alphabet verschoben wird. Beim achten Zeichen wird wieder um eine, beim neunten um fünf etc. verschoben. Das Vigenère-Verschlüsselungsverfahren galt fast dreihundert Jahre als unknackbar.
Oft wird der Schlüssel dabei nicht durch eine Zahlenfolge, sondern durch die entsprechenden Buchstaben des Alphabets dargestellt – in oben stehendem Beispiel also durch „AELDHGK“. Damit lässt sich das Ersetzen der Zeichen (durch ein „Addieren“ der Positionen im Alphabet) auch viel einfacher programmieren.
Was ist ein Regler?
Im Unterschied zu einer Mikrocontroller-Steuerung, bei der ein Aktor auf einen vorgegebenen Wert eingestellt wird (beispielsweise eine LED auf einen Helligkeitswert oder ein Encoder-Motor auf eine bestimmte Position), sorgt ein Regler automatisch dafür, dass eine Zielgröße auch bei Störungen eingehalten wird (beispielsweise ein Spurfolger auch in einer Kurve der Spur weiter folgt).
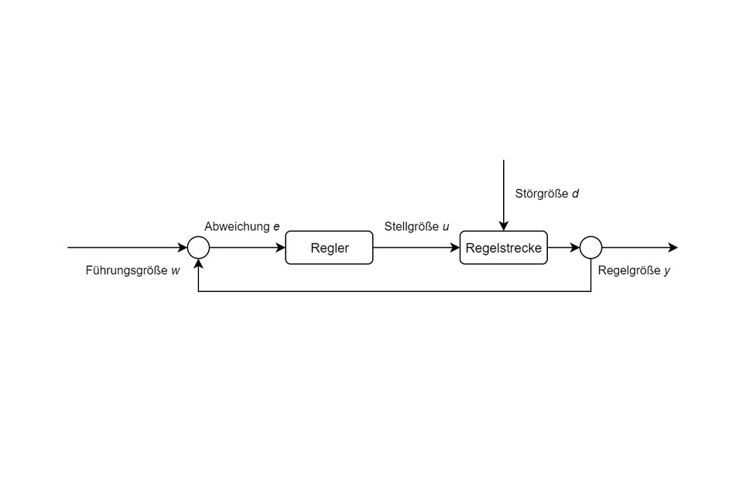
Dazu benötigt der Regler einen „Feedback“-Mechanismus, der ihn informiert, wenn es zu Abweichungen von der vorgegebenen Führungsgröße kommt. Schematisch lässt sich ein Regler wie in der folgenden Abbildung darstellen:
Bei einer Abweichung der Regelgröße von der Führungsgröße (der Vorgabe) korrigiert der Regler durch die Änderung einer Stellgröße nach, um die Abweichung zu verringern. Will man beispielsweise die Zahl der Umdrehungen einer motorgetriebenen Achse pro Zeiteinheit auch unter sich ändernder Last konstant halten, muss man die Umdrehungen messen und bei Abweichungen die Spannung des Motors erhöhen oder senken.
Bei der Regelung werden verschiedene Möglichkeiten unterschieden, wie die Abweichung in die Änderung der Stellgröße einfließt: So erfolgt die Korrektur bei einem Proportionalregler (auch P-Regler) im Verhältnis der Stärke der Abweichung. Schwingt der Regler über, d. h. sorgt eine verzögerte Wirkung der Regelung dafür, dass die Korrektur zu lange erfolgt, kann man die Regelung mit einem zusätzlichen Differentialglied (auch D-Glied) dämpfen, das die Änderung der Abweichung berücksichtigt. Damit wird bei einer plötzlichen starken Störung die Regelung verstärkt, bei einem schnellen Rückgang der Abweichung die Regelung abgeschwächt.
Ein integrierender Regler (I-Regler oder I-Glied) berücksichtigt außerdem die Dauer der Abweichung, indem er die Summe der gemessenen Abweichungen in die Korrektur einfließen lässt und damit die Annäherung an den gewünschten Wert beschleunigt.
Bei der Konstruktion eines geeigneten Reglers ist die Bestimmung der Faktoren, mit denen die in die Regelung einfließenden Werte (Abweichung, Änderung der Abweichung, Summe der Abweichungen) multipliziert werden müssen, um den gewünschten Regelungseffekt zu erzielen, die größte Herausforderung. Sie gelingt oft am schnellsten experimentell. Üblicherweise beginnt man mit der Bestimmung des Faktors für das P-Glied und wählt diesen so, dass der Regler gerade nicht oszilliert (das Überschwingen also abnimmt). Dann ergänzt man den Faktor für das D-Glied und beginnt zunächst mit einem sehr kleinen Faktor, den man langsam vergrößert, bis das Einschwingen auf die Führungsgröße schnell genug erfolgt.
Beim I-Glied ist zu beachten, dass man die Werte der Abweichungen nicht dauerhaft aufsummiert (also z. B. nur eine begrenzte Zahl von zurückliegenden Abweichungen berücksichtigt oder vor der Addition der nächsten Abweichung den alten Summenwert verkleinert, z.B. durch einen konstanten Wert dividiert), da das I-Glied sonst sehr schnell die P- und I-Komponente dominiert.
Ein Regler mit P-, D- und I-Glied wird auch als PID-Regler bezeichnet.
Download der ROBO Pro Coding App
Bevor es losgeht, muss noch die ROBO Pro Coding App heruntergeladen werden. Einfach das passende Betriebssystem auswählen und auf den Link klicken:
Download Voice Control
Dem Roboter sagen, wo es lang geht! Einfach unsere Voice Control App herunterladen und dem Roboter individuelle Befehle geben:







